La température (3) : modulation d'amplitude
- Analyse brute (de pomme)
- Découpage en 4 bandes
- Variation quotidienne de la température : modèle en modulation d'amplitude
- Variation quotidienne de la température : ajustement style modulation de fréquence
- Variation quotidienne de la température : et pourquoi pas un modèle en modulation du rapport cyclique jour/nuit?
- Synthèse en modèle simplifié de la température (pour des usages bateaux)
Aujourd'hui, nous continuons notre farfouillage dans la boite à outils du côté des tournevis, euh, je voulais dire, de la modulation AM.
Au passage, petit clin d'oeil à l'annuaire des radios de France :-)
2.2- Modèle journalier n°2/4 : modulation d’amplitude
En principe, ça se reconnaît à l’oeil en regardant l’enveloppe de la variation journalière.
Modulation AM (GIFanim, crédit : http://mriquestions.com/signal-squiggles.html )
Pour commercer, on revoit rapidement le cas le plus simple : un sinus modulé en amplitude par un sinus. Le classicisme le plus pur, quoi !
On va prendre les notations suivantes :
y(t) = Aj.(1-h.cos(ωm.(t-tm))).cos(ωj.(t-tj))
Pourquoi ce choix ?
La notion de température mini/maxi pendant la journée se ressent bien plus facilement que celle de température moyenne, d’où le choix du cos() plutôt que sin(). En particulier, on ressent facilement le maxi de température en journée, d'où une forme +cos(). Ben oui, le mini de température survient pendant la nuit. Je ne sais pas vous, mais moi, la nuit, je dors.
Pour la modulation, on a fait le choix de privilégier un retard de phase tm « petit », donc une forme -cos().
Modulation AM triviale
Pour l'illustration ci-dessus, nous avons :
- porteuse pure Aj=1, fj=1, tj=4 heures
- modulation pure h=0,4, fm=15 jours, tm=2 jours
Dans le domaine fréquentiel, le signal modulé apparait composé de 3 raies (sachant que tout est "dupliqué" côté fréquences négatives) :
- La porteuse de fréquence fj et puissance Aj²/2
- Deux raies en miroir autour de la porteuse, pour une puissance cumulée de 2*(Aj².h²/4)/2
- puissance totale du signal : Aj²/2 + Aj².h²/4 = Aj²/2 * (1+h²/2)
valeur efficace Aj/√2 . √(1+h²/2)
| Le spectre de y(t) s’obtient directement en développant l’expression de y(t) : y(t) = -Aj.cos(ωj .(t-tj)) + Aj.h/2 * ( cos((ωj-ωm).(t – t-) + cos((ωj+ωm)(t - t+)) ) avec, pour être complet :t- = ( ωj .tj – ωm.tm) / (ωj - ωm) |
Évidemment, dans la vraie vie, il est peu probable que l’on tombe pile poil sur un sinus pur modulé par un sinus pur!
Pour une modulation g(t) quelconque et une porteuse périodique yj(t) quelconque de fréquence fj, on retrouvera à l’identique la même modulation g(t) en miroir autour de chaque harmonique de fj, à un facteur près.
Hein? Keskidit?
Atta, avec une formule et une schéma, c's'ra plus clair :
| modulation | g(t) |
| porteuse | yj(t) = A1.raie1 + A2.raie2 + ... |
| porteuse modulée | y(t) = (1+g)*yj y(t) = (1+g).A1.raie1 + (1-g).A2.raie2 + ... |
harmonique k de la porteuse | raiek(t) = cos(2k π .f j .(t-t k )) |
Forme générale du spectre d'une modulation d'amplitude
| y(t) = (1+g(t))*yj(t) = (1+g(t)) * ∑ A k .cos(2k π .f j .(t-t k )) Calcul trivial : chaque harmonique de y(t) est modulée exactement de la même manière que la fondamentale. En travaillant sur signal centré, on impose A0=0, ce qui permet de s’affranchir proprement des images de la modulation autour de 0. Sur signal réel, cela évite par construction de mélanger les vraies variations lentes de y(t) avec une éventuelle modulation AM en f j . y (t) = Re[ A 1 .(1+g(t)) * ∑ α k . e 2 j kπ.fj.(t-t 1 ) ] avec k ≠ 0 , α k = 1, et α k, = A k / A1 * e 2 j kπ.fj.(t 1 - tk ) Le « facteur-près », c’est α k , un coefficient complexe qui exprime à la fois l’amplitude relative A k /A1 de l’harmonique k , et son retard relatif t k -t 1 |
A ce propos, on se retrouve avec les puissances suivantes :
- pour la fondamentale modulée P1 = A1²/2 * (1+geff²)
- pour l’enveloppe démodulée Penv = A1².(1+.geff²), en gardant à l'esprit qu’elle contient une composante continue d’amplitude A1
Tout ça, c’est bien joli, mais comment va-t-on appréhender tous ces paramètres ?
Et bien, comme un récepteur AM, pardi !
Attention, en faisant une détection crête, et non pas par détection synchrone !
En effet, on ne peut pas supposer que la porteuse est parfaitement périodique de période 1 jour. C’est une impossibilité physique, qui sera expliquée dans la section sur la modulation de rapport cyclique jour/nuit. Certes, on pourrait aller chercher une détection synchrone élaborée, qui contourne l’obstacle via une boucle à verrouillage de phase (PLL). Euh, honnêtement, on ne va peut-être pas aller jusqu’à couper les cheveux en quatre dans le sens de la longueur, quand même...
Une détection crête travaille sur les minis-maxis de la porteuse. Si on ne dispose pas des mini-maxis journaliers, on peut les bricoler à partir du relevé :
temp = matrix(temp,Pj,365); figure ( 60 ) ; |
Au passage, petite astuce de programmation scilab : comme on manipule un relevé régulier toutes les X minutes, le vecteur de la température journalière est ici ré-arrangé en matrice où chaque colonne regroupe les températures de la journée. On peut alors extraire en parallèle les minis et les maxis par colonne. Hop là !
Extraction directe des mini-maxis quotidiens
Dans la partie du haut, on retrouve bien dans les courbes Tmin et Tmax notre notion d’enveloppe crête à crête. On voit aussi que ces 2 courbes portent en elles la variation annuelle (+ des variations « lentes »). Tout ça ressemble furieusement à un signal différentiel dont on voudrait éliminer le mode commun. Bon, et bien, allons-y, Alonzo !
enveloppe = (Tmax-Tmin)/2; // demie-enveloppe ?
Au passage, on divise par 2 pour passer d’une amplitude crête-crête à une amplitude crête.
Le résultat? C'est la courbe du bas en magenta. Maintenant que nous avons une enveloppe, nous pouvons a priori en déduire Aj (valeur moyenne), h (amplitude centrée), fm (raie principale de la transformée de Fourier). Tout va bien, n ’est-ce pas ?
N’est-ce pas ?... 
(source : https://www.youtube.com/watch?v=UCBl-w2vprE)
(Coup de tonnerre… Le suspense monte…
Le rédacteur vient de rappeler sans ménagement au lecteur qu’il assiste à une acrobatie sans filet. Que va-t-il se passer ? Va-t-on assister à un retournement de situation ? Un protagoniste est-il en péril mortel ?...
Mais qu’y-a-t-il donc vraiment à l'intérieur de cette mystérieuse enveloppe ?…)
(source https://films-muets.blogspot.fr/2014/10/)
...Fondu au noir, flashback...
Nous avons fait une extraction des températures minis et maxis de chaque journée, en se calant sur l’heure légale à laquelle on change de jour (minuit). Tout ça sans précaution particulière.
Est-ce qu’on aurait dû en prendre, des précautions?
Oh que oui!...
Tout d'abord, il faut décaler les « fenêtres de tir », afin d'extraire les minis et les maxis sur des plages horaires qui font sens. C'est à dire des cyles de 24h à peu près centrés sur les horaires usuels de température mini et maxi, au lieu de se contenter de caler tout à minuit.
Pour s'en rendre compte, regardons la répartition de ce qu’on a extrait.  Aïe ! En regardant de plus prêt nos précédentes courbes de température, ce type d’erreur d’analyse se voit par exemple sur la journée n°184 : on loupe le vrai mini de température de la nuit 183 → 184. Pour Tmax, une extraction basée sur 0h→24h revient à considérer que l'horaire usuel des températures maxi est midi. L'histogramme montre que c'est suffisamment proche d'être le cas, d'où un résultat nettement plus potable pour l'extraction maxis quotidiens. Une première approche serait de centrer les fenêtres sur les gaussiennes ci-dessus. Soit une capture des minis centrée sur 6h, et une capture des maxis centrée sur 15h. Néanmoins, il faut être conscient que l’impact du déplacement des fenêtres ne se limite pas à la seule récupération des faux minis (et de quelques faux maxis) évoqués ci-dessus. On peut perdre au passage des vrais minis-maxis qui expriment une météo exceptionnelle (arrivée d'un front très chaud et orageux durant une nuit d'été, coup de mistral démarrant en milieu journée, ...). Autrement dit, on s'attend à ce que ce soit mieux calé, et c'est le plus probable, mais on n'a aucune assurance que ce sera calé au mieux. Une deuxième approche, plus optimale à peu de frais, est se payer le luxe d'un peu de bourrinage. C'est à dire passer tout ça au crible en vue de sélectionner le meilleur calage. C’est à dire tester chaque calage possible heure par heure en vue de minimiser le nombre d'erreurs -présumées- de type faux mini ou faux maxi. C'est à dire minimiser le nombre de mini (respectivement maxi) qu'on trouve aux bornes de la fenêtre horaire. C'est à...Ahem, c'est parti!
 Cette méthode se rapproche globalement d'une détection synchrone. Pour aller plus loin -mais on ne le fera pas, une troisième méthode est possible. Au lieu de chercher à minimiser le taux d’erreur global par un calage global, on peut chercher à travailler « au coup par coup ». C’est à dire, depuis l’extremum courant, rechercher le candidat pour le prochain extremum qui corrèle le mieux avec le fait qu’on l’attend environ 24h après, tout en éliminant/filtrant le « bruit » de mesure. Ça, ce serait typiquement le boulot d’une boucle à verrouillage de phase (une PLL en mode tracking, pour tout dire). Eurk! Trop compliqué! |
Pour le relevé sur lequel on travaille, le taux d’erreur apparaît minimal en calant l’extraction de Tmin à partir de 15-16h la veille, et Tmax à partir de 8h le matin. Cela nous donne la répartition horaire suivante.
// Recalage du démarrage des fenêtres d'extraction Kmin_depart = (16/24-1)*Pj; |
Répartition horaire des mini-maxis quotidiens après recalage des plages horaires d'extraction
Aaah, c'est mieux! Le héros de notre polar affiche un sourire satisfait, puis soudain, son visage se fige...
...Fondu au noir, 2e flashback...
Doute subit : au fait, formellement, que signifie « extraire les minis/maxis » ? Et qu’y a-t-il dans ce « mode commun » qui semble porter Tmin et Tmax ?
Formellement, le mini (respectivement le maxi) de chaque journée est récupéré, et le reste du signal est jeté. Cela s’appelle une décimation. Raaah, non, pas celle de Crassus et Spartacus !
| Tmin est ainsi un sous-échantillonnage à la fréquence moyenne 1/jour du signal température. Pourquoi parler de fréquence moyenne plutôt que fréquence -tout court. Parce qu’il y a une différence avec une décimation classique. Dans celle-ci, on sélectionne un échantillon selon une période stricte, ce qui revient à appliquer un peigne de Diract régulier. Pour Tmin, on sélectionne un extremum sans se préoccuper de quand il se produit, ce qui revient à appliquer un peigne de Dirac irrégulier (la période des dents présente une variance). Bien évidemment, le peigne de Dirac de Tmax est lui aussi irrégulier, et ce n'est pas le même que celui de Tmin, et il démarre avec un autre calage que Tmin comme nous l'avons vu dans le précédent encadré. Mmouais ?… C’est juste une idée comme ça ou bien ? "Ou bien" Tout d'abord, étendons un poil notre travail sur le recalage de l'extraction des minis-maxis.
Ces valeurs nous servirons un peu plus loin. |
N'oublions pas que Tmax et Tmin sont la même température à environ 1/2 journée près.
A titre indicatif, on peut calculer ce délai moyen entre mini & maxi et son écart-type à partir de s rangs absolus (Kmax+ K max_depart)-( Kmin+ K min_depart) , ainsi que l’heure moyenne à laquelle on est à mi-chemin entre le mini et le maxi du jour (et son écart-type) :
- Retard des maxis sur les minis :
hmaxmin = 9h49 ± 4h50 - Horaire moyen du « passage par 0 »
h0 = 10h30 ± 2h17
Revenons à la décimation proprement dite. On se doute bien qu’on y laisse des plumes (comprendre : de l’information), vu qu’on a éliminé plein de points de mesure pour obtenir Tmin et Tmax.
Regardons de plus près si, comment, et jusqu’où les variations « lentes » de température passent dans Tmin et Tmax.
| Nyquist et Shannon n’étant jamais loin, la bande passante d’un signal sous-échantillonné est au mieux la moitié de la nouvelle fréquence d’échantillonnage. Soit, dans notre cas : f2j = 1/2 * fj = 1 / (2 jours) Aux fréquences basses, loin de f2j, toute cette partie de signal passe nickel . A proximité de f2j , on se heurte à la fois au critère de Shannon standard, et à la variance des pseudo-périodes d’échantillonnage de Tmin et Tmax. La limite peut être estimée par un simple calcul d’incertitude basé sur l’horaire des minis : f2j (T min ) = ( 24h + Δhmin )/2 ⇒ Δf2j (Tmin )/f2j (Tmin ) = Δhmin / 12 ... et respectivement pour Tmax. |
Avec les chiffres précédents, les limites de bande passante utile de Tmin et Tmax se situe respectivement vers :
f2j (Tmin ) = 182,5 ± 30.5 « fois par an »
f2j (Tmax) = 182,5 ± 19 « fois par an »
Sous ces fréquences, Tmin et Tmax embarquent intactes les variations lentes de la température. Le voilà, notre « mode commun » !
Attention, ces variations lentes sont certes issues du même signal température, mais capturées à des instants différents.
Je sais, je radote, on va dire que c'est un effet de bord des cheveux qui blanchissent, na!
| Tout d’abord, faisons un petit peu de travail sur la notation, tout en revisitant les bases. TC(f) = ∑t:0→N-1 temp_centree(t).e - j.2 π. f.t/N pour -N/2 ≤ f ≤ N/2 La transformée inverse nous donne une écriture du signal dans le domaine temporel à partir de ses raies : temp_centree( t ) = 1/N. ∑f:- N/2→N/2 TC(f) . e j. 2π . f.t /N pour 0 ≤ t < N Le signal est à valeurs réelles, donc sa TFD est paire à symétrie hermitienne. En notant θ(f) la phase de la composante Tc(f), on aura : |TC(f)| = |TC(-f)| Rappelons aussi qu'on travaille sur signal centré, donc TC(0) = 0. On empile tout ces trucs de façon à regrouper les composantes en -f et f : temp_centree(t) = 1/N . ∑f:1→N/2 |TC(f)|.-e -j.θ (f).e -j.2π.f.t /N + |TC(f)|.e j.θ(f).e j.2π.f.t/N pour 0 ≤ t < N D’où, enfin : temp_centree( t ) = ∑f yf(t) Ok, ok, j’avoue, toute cette java calculatoire visait surtout à justifier proprement la décomposition du signal température en cosinus |
On considère que le signal temp_centree(t) satisfait au critère de Shannon.
Ok, ok, dit comme ça, c'est un peu pompeux. En langage plus clair et moyennant plus de souffle et de salive, ça signifie qu'on a, pour la composante du signal dont la fréquence fmax est la plus haute, et un échantillonnage de fréquence N : fmax ≤ N/2. Au fait, j'l'ai dit que la fréquence N/2 (eqv au double de la période d'échantillonnage) est appelée fréquence de Nyquist? Ou pas? Enfin bon, voilà, c'est dit.
Euuuh... C'est une supposition gratuite, le respecter le critère de Shannon?
Ahem, c’est pas comme si on avait le choix! Ah oui, tiens, c'est vrai qu'on n’a pas abordé le sujet jusqu’ici. Cela revient à supposer que le système de mesure (capteur et électronique derrière) fait son boulot proprement. C’est à dire qu’il filtre convenablement passe-bas sous la fréquence de Nyquist avant d’échantillonner.
| Conséquence importante : signal échantillonné temp_centree(t) en temps discret ou signal d'origine temp_centree(t) en temps continu, c'est bonnet blanc et blanc bonnet! Et si l'acquisition ne respecte suffisamment pas la fréquence de Nyquist? |
Bien, on a planté le décors, il nous reste à comprendre ce qui se cache dans notre calcul naïf :
enveloppe = (Tmax-Tmin)/2; // demie-enveloppe ?
| Considérons la raie yk(t) de fréquence k<<f2j , qui fait partie du « mode commun » qu’on cherche à décortiquer. Comme déjà dit, elle ne subit pas de repliement de spectre lors des décimations amenant à Tmin et Tmax. On la retrouve intacte dans la décomposition en cosinus de Tmin et Tmax, dont on a dit qu'ils sont une version tronquée (décimée) du même signal d'origine : Tmin(k,t) = Tmax(k,t) = temp_centree(k,t) = yk(t) = Yk .cos( 2 π . k / N.( t- tk ) ) CQFD ? Ah-ah ! Pas tout à fait ! Tmin(k ,t) représente ici la raie de fréquence k à la date t du signal support reconstruit après décimation. La vraie date t en temps continu, dans la même échelle de temps que le signal d’origine. Et non le t-ième sous-échantillon de Tmin, qu'on devrait noter Tmint (ou plutôt Tminn pour éviter les emmêlages de pinceaux). Comme quoi, faut rester vigilant sur les raccourcis de notation... tn ~ (n + hmin/24). Pj On a ici un changement d'échelle du temps discret tn (suite de dates vraies) vers n (rang de l'échantillonnée = suite de dates normalisées de Tmin). Allez hop, on généralise en temps continu, en mettant de côté la variance de hmin, puis regardons ce que ça donne pour notre raie k : Posons t' = t.fj - hmin/24 ⇔ t = (t' + hmin/24).Pj Allez hop, on va généraliser ça en temps continu, de façon sur nos pa-pattes. C'est à dire trouver l'expression Tmin(k,t') où t' est tel que Tmin(k,t'=n) = Tminn (à la variance près sur hmin). Pour quoi faire, tout ça? Le but n'a pas changé : vérifier ce qui se cache dans la fameuse "enveloppe" mini-maxi. Posons t’ = t.fj - hmin /24 Et là, pour le coup, on a bien Tmin(k,t’) = Tmint’(k). A la variance sur hmin près, oui, je sais. t" = t.fj - hmax/24 Maintenant, et maintenant seulement, nous sommes capables de reconstruire la soustraction naïve faite sous scilab. Allez, on chante le refrain tous ensembles : "à la variance sur hmin près". ½ ( Tmaxn(k) - Tminn(k) ) |
Rablam ! 
En mélangeant naïvement des mini et maxis pris à des dates différentes, on obtient un mélange de bon et de n'importe quoi.
Dans le bon, le « mode commun » qu'on voit intuitivement dans les courbes de Tmin et Tmax sous scilab existe bel et bien. Il représente les fréquences k<<f2j du signal d’origine. En faisant une soustraction naïve, on cherchait à s'en débarrasser et conserver uniquement la variation au cours de l'année de l'amplitude quotidienne de la température (modulation AM sur porteuse "jour"). Bref, on voulait obtenir 0 pour tout k<<f2j, et à la place on obtient le résidu sinusoïdal suivant :
Yk.sin(2π.k/365.hmaxmin/24/2).cos( 2π.k/365.(n - (tk.f j - h0/24 - 365/k/4)) )
où
n : rang du jour
hmaxmin : écart moyen entre les horaires des mini et maxi de la journée, en heure
h0 : horaire moyen du « passage par 0 » de la variation journalière (= mi-chemin entre l'horaire du mini et celui du maxi de la journée), en heure
Pas convaincu(e) ?
C’est bien compréhensible après tant d'acrobaties calculatoires sans filet.
No problemo, on va illustrer et confronter la théorie avec la pratique 
Choisissons une raie k quelconque (*) de la température centrée. Quelconque, ça veut dire qu’on évite les fréquences dont la période est un multiple des raies de la journée ou de ses harmoniques significatives.
Pourquoi ?
Hé hé… « Patience petit scarabée », on en causera un peu plus loin.
| // sélection d'une raie k quelconque et périodes des subharmoniques et harmoniques d'intérêt, au cas où... // (avec un calcul en k-1 vu que Scilab démarre ses indices à 1) k = int(365/2/%pi^2); → (365*[.5 1 2 3 4 5])/(k-1) ans = 10.735294 21.470588 42.941176 64.411765 85.882353 107.35294 |
| // Extraction de la raie de fréquence k- 1 << f2j=365/2 // « La raie » k est prise sur le spectre de la température centrée TC = fft( temp)/ N; // En fait, o n conserve non pas une mais deux raies : en k // et -k (sous scilab, cette dernière se trouve dans la partie // f:N/2→ N du spectre ) Y = [zeros(1 ,k-1) TC( k) zeros(1 ,N-2* k+1) TC( N- k+2) zeros(1 ,k-2)] ; Yk = abs( Y( k))*2 ; tk = -phasemag( Y( k))/360* N/( k-1)+1 ; // notre tout premier échantillon tombe à minuit + 1 période // On revient dans le domaine temporel yk=ifft( Yk) ; disp([ Yk tk/ Pj] ,'Yk, tk/Pj') ; // Extraction des contributions aux minis-maxis et calcul du résidu correspondant (en valeur relative) // Les fenêtres de décimation qui donnent les rangs K___ ont préalablement été calées au mieux mc_avec_variance = ( yk((0:364)* Pj+ Kmax_depart+ Kmax )- yk((0:364)* Pj+ Kmin_depart + Kmin ))/2/ Yk; mc_sans_variance = ( yk((0:364)* Pj+ Kmax_depart+mean( Kmax))- yk((0:364)* Pj+ Kmin_depart+mean( Kmin)))/2/ Yk; // On affiche en valeur relative dans le domaine temporel… figure() ; xgrid ; plot( mc_sans_variance*100 ,'r') ; plot( mc_avec_variance*100 ,'b') ; xtitle('Résidu d''une raie du mode commun dans la pseudo-enveloppe' , 'Jour' , 'Amplitude relative (% = d°C/°C)') ; // ...puis dans le domaine fréquentiel MCSV=fft( mc_sans_variance)/365 ; MCAV=fft( mc_avec_variance)/365 ; figure() ;xgrid ; plot(0:364 ,abs( MCSV)*100 ,'r') ; plot(0:364 ,abs( MCAV)*100 ,'b') ; xtitle('Spectre de ce résidu (en relatif à l''amplitude de la raie d''origine)' , 'Fréquence (par an)' , 'Magnitude relative') ; // Vérification du calcul théorique vis à vis des courbes obtenues // Attention, pour le mode commun sans variance, il faut recalculer hmaxmin et h0 sans variance itou, // sachant que scilab a interprété ci-dessus les indices non entier mean(K___) comme l'entier inférieur hmaxmin = (int(mean( Kmax))-int(mean( Kmin)) + Kmax_depart- Kmin_depart )/ Pj*24 ; h0 = (int(mean( Kmax))+int(mean( Kmin)) + Kmax_depart+ Kmin_depart)/2/ Pj*24 ; MCSVk = abs ( MCSV ( k )) * 2 ; MCSVk_th = sin(2*%pi*( k-1)/365* hmaxmin/24/2) ; mcsv_tk = - phasemag ( MCSV ( k )) / 360 * 365 / ( k - 1 ) ; mcsv_tk_th = tk/ Pj- h0/24-365/( k-1)/4 ; // modulo la période pour une valeur au plus proche de 0 mcsv_tk_th = mcsv_tk_th-365/( k-1)*round( mcsv_tk_th*( k-1)/365) ; disp([ MCSVk_th MCSVk] , 'Amplitude relative du résidu (hors variance) : théorique, mesuré') ; disp([ mcsv_tk_th, mcsv_tk] ,'Retard du résidu (hors variance) : théorique, mesuré') ; |
Qu'est-ce que ça donne?
Résidu de mode commun de la raie f=17 fois par an, dans le domaine temporel, hors variance de h0 et hminmax (en rouge) et avec (en bleu)
Hors variance, le résidu de mode commun a bien la forme d’une sinusoïde (avec du bruit quand on intègre la variance). On va vérifie ça plus finement dans le domaine fréquentiel.
Résidu de mode commun de la raie f=17 fois par an, dans le domaine fréquentiel
L’ analyse de Fourrier confirme l'intuition précédente.
- La sinusoïde hors variance est une raie parfaite.
- En réintégrant la variance sur les minis-maxis, on obtient exactement la même raie
- la variance se transforme de façon remarquable en bruit blanc.
Attention, ça ne donne pas carte blanche pour généraliser et affirmer que la variance sur les horaires des minis-maxis se traduit par un simple bruit blanc sur l’hypothétique modulation AM recherchée! En effet, cela dépend de comment s’additionnent les bruits remontés par chacune des raies. Au besoin, il faudrait vérifier raie par raie (pénible et pas crucial).
Pour finir la validation du calcul analytique, qui m'a coûté quelques gouttes de sueur et quelques heures de sommeil pour la gestion rigoureuse des indices, voici les résultat pour la fréquence ci-dessus (hors variance sur l’emplacement des minis-maxis ) :
- Yk = max(yk) = -min(yk) = sum(abs(Yk))/N = 0,61 °C
- tk = 2.95 jours
- Amplitude relative de la sinusoïde du résidu : 6%
identique entre calcul analytique et mesure - Retard de la sinusoïde du résidu : -2,84 jours
identique à un modulo près entre calcul analytique et mesure
Revenons sur l'expression formelle du résidu de mode commun, dont on sait maintenant qu'elle est solide. Mettons de côté les histoires de Nyquist = 365/2, ça simplifiera un peu la causerie.
L’amplitude relative du résidu est portée par le sinus. Elle empire en fonction de la fréquence, jusqu’à atteindre son maximum à la fréquence f=365/2*24/hmaxmin= 445 « fois par an ».
Si les minis-maxis étaient idéalement répartis toutes les 12h, ce maximum tomberait pile sur f=fj=365 fois par an.
Bon, ben j'crois qu'c'est clair. Tminn et Tmaxn ne sont pas du tout les 2 facettes d’un signal différentiel au même instant, pour lequel il suffit de faire une soustraction pour virer le mode commun sans autre forme de procès. Tmin et Tmax sont asynchrones. Et notre soustraction naïve pour le calcul d’enveloppe a introduit un sacré « résidu d’asynchronisme ». Fondamentalement, cette perturbation fausse l'extraction de l’enveloppe réelle, et affecte tout le spectre, pas uniquement les fréquences inférieures à f2j pour lesquelles on a fourni le calcul pas à pas.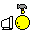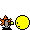 
Pour éliminer correctement le mode commun, il faut :
soit le faire sur le signal d’origine avant changement d’échelle de temps, donc en filtrant avant décimation. Reste alors à gérer proprement l’asynchronisme entre Tminn et Tmaxn
soit le faire sur les signaux reconstruits Tmin(t) et Tmax(t) en temps vrai, qui réintègrent les dates exactes des minis et maxi et sont pour le coup synchrones. Et là, ça devient une vraie paire différentielle exprimant l'enveloppe de la modulation AM portée par le mode commun des variations lentes de température .
Voilà, le tableau semble brossé, l'affaire pliée. Pourtant, une impression sourde, persistante. Quelque chose qui ne colle pas dans ce tableau trop parfait. Le regard du héros de notre polar se plisse. Il tend l'oreille. Qu'est-ce? Un bruit anormal? L'écho d'un signal entre comparses? Mais oui, c'est ça! Cela lui revient en mémoire...
...Fondu au noir, 3e flashback...
Dans l'extraction de Tmin et Tmax, nous avons pris sans précaution particulière des points à peu près régulièrement. Pas de pré-traitement ni de post-traitement. A-t-on vraiment le droit de faire ça ?
:-D Le Droit oui, cher Maître ! Euh, pour la légitimité, c’est assez gauche…
Vous souvenez-vous des des effets moirés des vêtements à rayures fines ou pied-de-poule de Roger Gicquel ? Ou Yves Mourousi, Christine Ockrent, etc. Quoique, dans mon lointain souvenir, les costumières de ces dames étaient souvent plus avisées!
source : http://www.astrosurf.com/luxorion/Physique/moire-colored.jpg
Ce sont des artéfacts d'aliasing : des mirages dus à l’expression de fréquences visuelles trop haute pour la chaine de traitement du signal vidéo de l’époque. Dit autrement, le signal (optique) emplafonne la fréquence maxi de l’échantillonnage (Nyquist). C’est un effet de bord de la décimation, au sens propre du terme : elle replie dans la bande de base tout ce qui, dans le signal d’origine, dépasse la fréquence de Nyquist de l'échantillonage.
De façon générale, pour éliminer les artéfacts, il faut filtrer.
La technique usuelle, quand on veut faire une décimation, est de filtrer passe-bas avant de décimer, à -maxi- la moitié de la fréquence du sous-échantillonnage.
| Qualitativement, tout ça se comprend certes fort bien. L’illustration ci-dessus représente surtout ce qu’il se passe pour un échantillonnage. Elle rappelle -avec un joli origami- qu’un signal périodique discret n’est pas représenté dans le domaine fréquentiel uniquement par son spectre entre 0 et la fréquence limite de Shannon-Nyquist. Les images de ce spectre « de base » s’étendent à l’infini. L’infini des fréquences positives, et l’infini des fréquences négatives. En fait, pour le repliement, il faut voir la feuille dans l’illustration ci-dessus comme un calque plutôt que comme une feuille de papier opaque. Bref, sauf cas simple-mais-pas-tant-trivial (genre décimation par 2), le calcul analytique du cas général devient très très vite l’horreur, car on ne peut pas se restreindre à un calcul sur la bande de base avant décimation. Tiens, autre effet -invisible sur la photo néanmoins très réel : le bruit haute fréquence lui aussi est replié et réinjecté dans la bande de base. Chplof ! Le pré-filtrage n’est pas magique. Il ne peut pas éviter la remontée du plancher de bruit. Par contre, il limitera cette remontée au strict inévitable. Quand on fait du traitement de signal ± temps réel, ce qui n’est pas notre cas, il n’est pas très efficace de tout filtrer pour ensuite décimer/jeter plein de résultats de filtrage. Au lieu de ça, on se borne à filtrer uniquement aux dates de la ré-échantillonnée. On parle alors de filtre polyphase. Joli nom, n’est-ce pas ? Pour info, il existe un problème similaire à celui de la décimation, quand on sur-échantillonne un signal discret (oversampling). Le suréchantillonnage étend la largeur de la bande de base, et repousse la fréquence de Nyquist. Au lieu de replier notre calque-origami à un pas plus petit, il est replié à un pas plus grand. Ah oui, tiens, ouvrons une parenthèse à ce sujet. Le délire des zooms magiques dans les séries TV est devenu usuel (surtout dans les séries policières américaines). A force de matraquage et banalisation, je crains que certains commencent à croire que c'est une réalité, surtout chez les professions juridiques qui généralement ne pannent que dalle en sciences & ingénierie... Bon, alors, remettons les points sur les i et les barres aux t. Certes, des algorithmes existent pour récupérer un peu de netteté sur une image zoomée, mais il faut être conscient qu’ils inventent -littéralement- de l’information qui n’existe absolument pas dans l’image initiale. Et utiliser une méthode bourrine à coup de réseaux neuronaux/IA pour récupérer beaucoup de netteté, ben, ça ne change strictement rien à la théorie du signal sous-jacente. C'est de l'invention au doigt mouillé d'une information qui n'existe pas à l'origine = pifométrique. Pour une vidéo, la situation est différente. Les images d'une séquence sont corrélées. Cela permet de piocher de la vraie bonne information ailleurs que dans l'image qu'on cherche à zoomer. Ne rêvez pas, ce n'est pas miraculeux comme dans les films ou à la télé. J’en profite pour glisser quelques liens :
|
Revenons à nos moutonsssss, comme dirait Topaze. Dans notre extraction naïve des Tmin et Tmax, sans s’en rendre compte, nous avons fatalement introduit de l’aliasing. Beuark !
La technique usuelle serait de préfiltrer à f2j avant d’extraire les minis-maxis. Cette technique est-elle appropriée pour notre but, à savoir extraire l’enveloppe ?
Naaaan…
Voici ce qui se passe quand on fait une décimation propre selon la technique standard.
Préfiltrage normal avant décimation
Le pré-filtrage à fréquence f2j avant décimation à la fréquence fj conserve les variations lentes de la température, et supprime le reste, y compris la modulation AM autour de fj. Ah ben zut alors, nous qui voulions justement récupérer la modulation AM, on est marron!
Puis la décimation change la fréquence d’échantillonnage, et fait apparaitre des répliques en f=k*fj du « mode commun » de Tmin et Tmax à l’infini. Comme on a pré-filtré, pas de repliement autour de fj, car plus de spectre à replier.
Résultat de la décimation après préfiltrage normal
Ah mais, ce n’est pas du tout ce qu’on veut, ça !
Ce qu’on veut, c’est récupérer la modulation AM, pas le mode commun. Ladite modulation est exprimée dans le signal d’origine de part et d’autre de fj, et à l’identique -à une phase près- autour des harmoniques de fj.
Allez...Hop ! On déplace le pré-filtrage là où ça nous intéresse.
Préfiltrage centré sur la zone d'intérêt avant décimation
Au passage, exit le « mode commun » qu’on retrouvait dans Tmin et Tmax.
On procède ensuite à la décimation, qui replie les fréquences à f2j. Là aussi, suite au pré-filtrage, il n'y a plus rien d’autre à replier que la modulation qui nous intéresse. Pas d’aliasing à l’horizon. Le changement de fréquence d’échantillonnage fait apparaître les répliques à l’infini, en particulier en f=0.
Résultat de la décimation après préfiltrage sur la zone d'intérêt
Comme disent les Américains : « et voilà ! »
On vient de démoduler notre modulation AM, youpi!
Ahem, j'veux pas gâcher la fête, mais il y aurait comme qui dirait juste un tout petit bémol : cette belle mécanique ne fonctionne sans accroc que pour une décimation régulière.
Pour une décimation irrégulière :
- le pré-filtrage doit couper au moins au-delà de f2j+Δf2j
- il doit être symétrique autour de fj
- Et malgré ces précautions, il y aura forcément un peu de distorsion. La variance de l’horaire des extrema implique une variance sur les fréquences de repliement. Du coup, une même raie du signal d’origine participera à plusieurs raies de la décimée.
Illustrons un peu tout ça, avec la raie de la température de fréquence 184 « fois par an ». Elle est juste au-dessus de f2j = 365/2 = 182.5.
Raie f=184 fois par an, avant démodulation
Evidemment, à l'origine, c'est par définition une sinusoïde parfaite, d’amplitude relative 50 % (l’autre moitié est dans la raie f= -184 « fois par an »).
Appliquons maintenant la décimation qui correspond à l'extraction de Tmin du signal d'origine. Pour une meilleure lisibilité, on va mettre le résultat sous forme de barres plutôt que des courbes.
Repliement de la raie f=184 dans le domaine temporel, suite à la décimation donnant Tmin
La courbe bleue correspond aux rangs sans variance, c’est à dire prendre 1 échantillon de la raie f=184 toutes les 24h à l’horaire hmin. Il apparaît un battement, typique de deux raies très proches, ou d’une raie proche de la fréquence de Nyquist (ce qui est le cas). Un classique du genre.
En rouge, ce sont les points de la sinusoïde pris exactement aux horaires de chacun des minimas de Tmin. Soyons honnête, c'est le bazar... S’il n’y avait pas la courbe sans variance, on aurait bien du mal à identifier quelque chose à l’oeil. Par comparaison des courbes, on soupçonne un peu de distorsion, en plus du bruit.
Voyons ce que ça donne dans le domaine fréquentiel.
Repliement de la raie f=184 dans le domaine fréquentiel, suite à la décimation donnant Tmin
Pour la courbe hors variance, "c'est rassurant, la magie fonctionne" (© Sean Connery in Highlander II). La raie 184 est repliée autour de fj/2=182,5. Le repliement est parfait (amplitude 50%).
Pour la courbe avec variance, au voisinage immédiat de la raie principale, la raie s’étale en sinus cardinal (ou fonction de Bessel ?). Plus loin (f<172), la variance sur hmin génère un bruit d’aliasing « blanc ».
| Pour aller plus loin, il est possible de calculer l’impact d’une décimation sur le retard d’une raie, en remarquant que cos(2.pi.k/365.n) = cos(2.pi.(365-k)/365.n) quand n est entier. Bon jeu aux courageux... |
Nous venons de voir qu’avec un peu de soin, on peut démoduler sur Tmin seul. C’est typiquement ce que fait un récepteur AM par détection crête à 1 diode.
Du coup, que fait-on de Tmax ?
...Fondu au noir, flash-forward...
Le faucon Maltais
La tension monte. Le héros du polar vient de réunir les protagonistes. Il est sur le point de pointer les coupables...
Qu’y avait-il dans cette mystérieuse « enveloppe » ?
Comment en sommes-nous arrivés là? Qu'avons nous fait?...
- Une recherche des minis-maxis de la journée arbitrairement entre minuit et 24h, en supposant que cela représente les creux et les pics de température. Trop naïf : la météo n’est pas réglée comme une horloge légale. Le vrai creux survient parfois avant minuit, et le vrai pic après 24h (plus rare).
- Une extraction des minis-maxis sans aucun soin, conduisant à mélanger les variations lentes + la modulation recherchée et ses harmoniques + les variations rapides hors modulation. Avec en plus une remontée importante de bruit vu qu’il n’y a eu aucune prise en compte particulière du caractère irrégulier des décimations Tmin et Tmax (les rangs des minis-maxis ont été purement et simplement mis à la benne!)
- Pour finir, une soustraction Tmaxn - Tminn supposée supprimer le mode commun (les variations lentes), comme si Tmaxn et Tminn se produisaient au même moment, alors que ce n’est évidemment pas le cas. Avec pour résultat un mélange entre :
- un résidu du mode commun
- la modulation recherchée, mais avec de la distorsion
- et, comme ce dernier mécanisme s’applique de la même façon aux harmoniques supérieures :
- au niveau des harmoniques paires, un résidu replié dans la bande de base
- au niveau des harmoniques paires, on ramène le tout dans la bande de base, sans atténuation, mais avec distorsion
Au final, cette soustraction naïve revient à faire un pari sur :
- des variations « lentes » trèèèès lentes (ce qui est plutôt faux : on a des raies de premier ordre jusqu’à 1/f=18 jours, et de 2e ordre jusqu’à 1/f=3,5jours)
- une variation journalière trèèès pure (ce qui est presque vrai : l’harmonique 2 est de 2e ordre et sera gommée, l’harmonique 3 et de 3e ordre, et le bruit HF est relativement bas)
- l’absence de toute raie HF significative. Pour le coup, ce dernier pari est sans vrai risque, sinon ça veut dire que le système de mesure donne des températures comme une girouette!
Démodulation AM naïve et ses problèmes
Z-n exprime l’introduction d’un retard de n échantillons. Ici, pas de recalage, d'où Z-0.
Inutile de sortir les flingues et jouer des muscles! Après tout, à part l’innocence et « la faute à pas d’bol », personne n’est mort. 
Voici comment obtenir ce qu’on cherche de façon propre et efficace :
- pré-filtrage anti-aliasing de démodulation AM
- Travailler sur la variation journalière Tjour(t) plutôt que sur le signal complet temp_centree(t), c'est à dire filtrer passe-haut pour évacuer les variations de température trop lentes vs. variation quotidienne.
- Filtrer passe-bas pour travailler uniquement sur la zone d’intérêt, comme dans un vrai récepteur AM à détecteur crête. En clair, on vire les variations de température trop rapides.
A quelle fréquence de coupure, me direz-vous? Fastoche : "la même" que celle du passe-haut, en symétrique par rapport à fj. Logique, non?
- Faire un recalage global des fenêtres d’extraction de Tmin et Tmax, pour s’approcher un peu des bénéfices d’un détecteur synchrone à PLL, la complexité en moins.
- Extraire Tmin et Tmax ainsi que les horaires de ces minis-maxis
- Reconstruire une sur-échantillonnée de Tmax et -Tmin en utilisant leurs horaires, pour minimiser les effets de la variance de ces horaires
- Filtrer passe-bas pour lisser les 0 de la sur-échantillonnée. Autrement dit, un post-filtre anti-image.
- Et enfin amplifier à proportion des échantillons significatifs Tmax et -Tmin de la sur-échantillonnée, pour rétablir son amplitude
Honnêtement, c'est plus long et plus compliqué à dire qu’à visualiser ! Ben oui, en pratique, c’est juste une sorte de redresseur double alternance, à la sauce signal numérique.
Démodulation AM correcte et résultat des diverses étapes
Les recalages des fenêtres de détection crête ne sont pas représentés (triggers sur les hmin et hmax de chaque jour).
Le passe-bas final présente un gain Pj/2.
Avant d'embrayer bille en tête, revisitons le calage de nos fenêtres de détection. En effet, vu qu'on pré-filtre les variations rapides de la température, ça va jouer sur le calage optimal des fenêtres d'extraction de Tmin et Tmax.
A vue de nez, on devrait tomber aux environs de 5h du matin -12h = 17h la veille pour Tmin, et 14h -12h = 2h pour Tmax.
Taux d'erreur de détection des minis & maxis du jour courant selon le calage de hmin et hmax
Presque! L'optimum est ici de caler la fenêtre de Tmin à 18h la veille, et celle de Tmax à 1h du matin. On retrouve ces valeurs dans le code ci-dessous, lors de l'appel à la fonction TminTmax().
Nota bene : la fréquence de coupure fc=266 n'est pas un lapin sorti du chapeau. Elle vient d'ici. On y ajoute 1 dans le code ci-dessous pour simplifier l'écriture de la suite, vu que indices commencent à 1 sous scilab.
Pj = 144; function [Tmin, Tmax, Kmin, Kmax, Kmin_depart, Kmax_depart]=TminTmax(temp, hmin_depart, hmax_depart)
// Recalage du démarrage des fenêtres d'extraction
Kmin_depart = (hmin_depart/24-1)*Pj;
Kmax_depart = hmax_depart/24*Pj;
[Tmin,Kmin] = min(matrix([temp($+Kmin_depart+1:$) ; temp(1:$+Kmin_depart)],Pj,365),'r');
[Tmax,Kmax] = max(matrix([temp(Kmax_depart+1:$) ; temp(1:Kmax_depart)],Pj,365),'r');
endfunction// Préfiltrage anti-aliasing en vue de la démodulation AM // Extraction de la variation journalière (passe-haut) // Extraction des minis-maxis et de leurs rangs // Synthèse de la suréchantillonée de l'enveloppe, en utilisant les vrais rangs // Filtrage anti-image = passe-bas ""de même coupure" df0 que l'anti-aliasing // Tadaaaa! Env1 est l'enveloppe qu'on cherche à extraire |
Youpi, on tient enfin notre enveloppe !
Euh, et alors ? Et alors???...
Zorro est arrivéééééé... Sans s'presseeeeer...
Ah, oups, oui, la suite et fin.
Comme ça fait un moment qu'on pérégrine dans les prés, l'est temps de se rafraîchir.
Non, pas le gosier! La mémoire.
On vient de là : y(t) = (1+g).yj où yj(t) est la porteuse.
Nous sommes ici : enveloppe(t) = A1.(1+g(t))
On conclut la partie analyse AM de la température quotidienne comme suit :
- extraire la composante continue de l’enveloppe
A1 = mean(enveloppe) = 3.613 °C - récupérer la modulation, c'est à dire la forme normalisée et centrée de l'enveloppe
g = enveloppe/A1 - 1 = (enveloppe - A1)/A1
Cf ci-dessous, oups ou zut -comme vous voulez, il y a nettement de la surmodulation... - jeter un oeil sur le résidu
- et enfin, extraire les valeurs efficaces de tout ce beau monde.
Mûûûh? C'est quoi c't'histoire de résidu???
Bah, c'est les variations "très rapides" de température, qu'on avait jetées en pré-filtrant passe-bas avant extraction de l'enveloppe. Conrètement :
Tjour(t) = (1+g).yj + Tresidu(t)
Bon, fastoche, la porteuse, c'est notre sinusoïde de fréquence fj, yapluka, n'est-ce pas?
Euuuuh...
Z'oubliez pas 1 ou 2 choses, là? Comme un léger hic...
- Et la variance sur les horaires mini-maxis, mmmh? C'est-y quoi donc? Ben, c'est une variance sur l'horaire des extrema de la porteuse.
- rien ne prouve que la porteuse yj(t) hors variance est un sinus pur! D'après le spectre générique de la température, il y a des harmoniques pas tout à fait négligeables en fréquence 1/2 journée, 1/3 journée, ... Ca veut dire que la variation journalière est périodique sans être tout à fait sinusoïdale.
Là, on s'écarte de la modulation d'amplitude, et on touche plutôt à de la modulation de fréquence. Allez, à chaque jour suffit sa peine, on se réserve ça pour le prochain article!
