Calculs de cheminée : euréka? (dépression statique)

Publié le 19 novembre 2012 par Yoghourt

(à droite, le four à pain de Lescure, vers Banassac)

Les petits travaux de la cuisine avancent doucement. Promis, j'en causerai pour la fin de la semaine. D'ici là, suite à ce fil de discussion sur Futura-Sciences, je fais passer devant la mise au propre d'une partie de mes réflexions.

Dans le premier article de la série, j'avais évoqué tout un tas d'options :

Tuber ou pas
Jouer sur le diamètre du tubage
Isoler entre conduit maçonné et tubage
Enfin, en ultime ressort, recourir à un modérateur de tirage ou un extracteur

Tout ça étant à réfléchir en fonction d'une cuisinière bois A (que nous avons) ou d'une cuisinière bois B (que nous lorgnons ).

Ce coup-ci, on va commencer à faire le tri dans les options. A coup de hache de jet à double tranchant barbotée dans la remise du grand-père Ockham. Tranchante comme un rasoir; ça va de soi...
(Oui, bon, j'avoue, j'ai lu du Terry Pratchett ce week-end )

Pour cela, rien de bien nouveau sous le soleil, on va appliquer la bonne vieille méthode du brave Archimède, afin de déterminer la dépression statique dP du conduit. Son "tirage naturel", quoi.
Euh... Arrêtez de vous déshabiller. Je parlais de son théorème, pas de se mettre à poil dans la baignoire dégoulinante avant que de brailler en Grec...

Données de base

- Elève Ducobu, au tableau !

(Hein ? Quoi ? Si je baisse la tête l’air de rien, peut-être qu’il demandra à quelqu’un d’autre...)
- Allez , la classe attend.
(Oh oh, vite, vite, mon antisèche ...)

Débarassons nous de suite du catalogue de valeurs et formules sur lesquels les calculs numériques seront fondés...

Pesanteur terrestre g = 9.81.m/s²
[metgen] Masse molaire de l'air sec Ma = 28,965 46 g/mol
[metgen] Masse molaire de l'eau Mv = 18,015 28 g/mol
Atmosphère OACI à 230m d'altitude
- pression atmosphérique P_ref= 101325*(1 - 6.5e-4 * 230/288)^5.255 = 101 049 Pa
- Température T_ref= 15 – 230*6.5/1000 = 13.5°C
- Humidité relative hr_ref= 0%
  Pourquoi 230m?
  Pour quoi 230m? Parce que c'est l'altitude de mon chez moi :-)
  Oui, je sais, l'air réel n'est pas sec, et la température moyenne en hiver est plus basse que ça en Isère. On va retoucher ça un peu plus loin.
[ASHRAE /Tenwo01b] Pression de vapeur saturante

pour T<0°C, Pvsat = (1,0003+4,18e-8*Pref)*611,15 * exp((23,85 - T/333,7) * (T-273,15)/ (T+6,67))
pour T>=0°C, Pvsat =(1,0007+3,46e-8*Pref)*611,21 * exp((19,84 - T/234,5) * (T-273,15)/ (T-16,01))
(HDS.0) On assimile la vapeur d'eau dans l'air à un gaz parfait:
- pas de facteur d'augmentation de la pression partielle de vapeur d'eau
- on prend Z =1 pour le facteur de compressibilité
[metgen] Faction molaire de vapeur d'eau dans l'air humide
(en négligeant le facteur d'augmentation qui traduit que la vapeur d'eau n'est pas tout à fait un gaz parfait)
xv = hr * Pvsat / Pref
(HDS.1) Pour la masse volumique de l'air humide, on va prendre une formule [metgen] moins directe mais conceptuellement beaucoup plus juste que la classique formule de Magnus-Tettens :
ρ_ref = ρ_ah(P_ref, T_ref, xv_ref) = P_ref / (Z.R.T_ref) * Ma * (1- xv_ref*(1-Mv/Ma))
avec la constante des gaz parfaits R=8.3144621J/mol/K
avec la température T en Kelvin T = T°C + 273.15K
Cette formule, au Z près, s'obtient avec exactement le même type de gymnastique que dans l'article avec le calcul de la masse volumique dse fumées.
On va rafiner la température moyenne hivernale. Plutôt que de se lancer dans une recette à base de données climatiques brutes, je vous propose d'exploiter les données climatiques prémâchées de DRIAS.
Modèle Scampei > température moyenne > hiver > année de référence 1970 > zoom et clics. Royal
Résultat : T_ref = 3°C
La météo du coin n'est pas spécialement humide ni sèche en hiver. Sans originalité, on va prendre hr_ref = 80%
Dans ces conditions atmosphériques de référence,
- Pvsat = 761Pa
- xv = 80% * 761 / 101049 = 0.6%
- ρ_ah = 101049 / 8.31 / (273.15+3) * 28.97 * (1-0.6% * (1-18/28.97) =1.27 kg/m3

(justification HDS.0) Une petite justification fissa concernant l'assimilation de l'air humide à un gaz parfait : le calcul [metgen] de Z pour xv variant entre 0.2% et 1%, donne des valeurs entre 99,925% à -10°C et 0.99,985% à 45°C. C'est au-delà de la précision qu'on vise dans nos calculs (au mieux de l'ordre de 0.1%).

Dépression statique du conduit

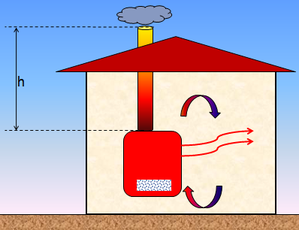
Voici la situation.

Notre appareil (A ou B) chauffe les fumées en bas du conduit, et on connait la température des fumées à cet endroit.

Le conduit fait une hauteur h.

Le haut du conduit est à l'air libre. Les fumées s'y équilibrent avec l'atmosphère ambiante.

Commes les fumées sont plus légères que l'air. Telle la montgolfière, elles cherchent à monter.

Qu'est-ce qui les y pousse? La poussée du pote Archimède.

Commençons par appliquer le théorème d’Archimède à une colonne d’air extérieur de section S et hauteur h :

Elle est à l’équilibre (la colonne d’air ne bouge pas).
Elle pèse S*h*ρ_ah
Elle soutient toute l’atmosphère au-dessus d’elle, et elle est soutenue par ce qu’il y a sous elle.
Le principe d’Archimède revient à dire qu’elle exerce une force de pression à l’altitude h égale à celle qui la soutient à l’altitude 0 diminuée de son propre poids.
Le bilan de force s'écrit alors :
S*P(h) = S*P(0) - poids
S*P(h) = S*Pref – ρ_ah*S*h*g

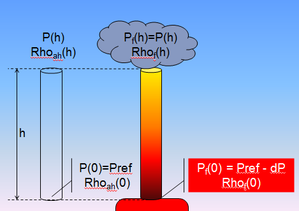
Avec l’approximation (HDS.1), on en tire la pression à l’altitude h :
P(h) = P_ref–ρ_ref.g.h

(justification de HDS.1) Si on mène le calcul sans cette approximation, on peut en déduire une valeur plus précise de la masse volumique moyenne qui intervient dans le poids de la colonne. Le calcul donne une différence très faible, de l'ordre de -2e-3 kg/m3. Négligeable.

(HDS.2) En haut du conduit, la pression des fumées est égale à la pression extérieure à la même altitude :

P_f(h) = P_e(h)

Dans notre cas d'étude simple, sans vent ni extracteur, ni même mouvement des fumées, on ne voit pas comment il puorrait en être autrement. Disons que la situation est comme s'il y avait une membrane souple entre la tête du conduit et l'atmosphère, et basta

On reviendra sur cette hypothèse dans un autre article, quand on en sera à causer tirage réel.

(HDS.3) On suppose de plus que la température moyenne du conduit de fumée est la moyenne arithmétique entre la température des fumées à la sortie de l’appareil Ts et la température extérieure T_ref. C'est à dire :

T_f(h) = T_ref

<T_f> = (T_f(0) + T_f(h))/2 = (Ts + Tref)/2
où <__> dénote la moyenne d'une grandeur.

Le profil des températures dans un conduit sera, a priori, plutôt logarithmique : beaucoup de pertes de chaleur par les parois au début, et moins au fûr et à mesure qu'on s'éleve puisque la différence de température s'amensuise.

Notre hypothèse reviendrait donc à surestimer la température moyenne des fumées. Une moyenne logarithmique semblerait plus juste. Oui, mais... D’un autre côté, en supposant que la température des fumées à la sortie du conduit est T_ref, on fait une estimation largement à la baisse de la température moyenne des fumées. L'un dans l'autre, c'est pour ça qu'on va conserver une moyenne arithmétique dans le calcul de la dépression statique.
On reviendra sur cette hypothése dans un autre article, quand on en sera à estimer plus finement la température réelle dans le conduit.

Blablabla théorème d'Archimède tout pareil en criant EUREKA dans la baignoire

P_f(h) = P_f(0) – <rho_f>.g.h

où <ρf> = ρf(<Tf>) est la masse volumique moyenne des fumées dans le conduit.

En appliquant l'hypothèse (HDS.2), on en tire le tirage recherché (ah! ah! je ne m'en lasse pas...)

P_ref– ρ_ref.g.h = (P_ref– dP) – <ρ_f>.g.h

dP = (ρ_ref - <ρ_f>).g.h

Tadaaaaaa....
Sans surprise aucune, on tombe sur la formule magique du "tirage naturel d'une cheminée". Sans surprise, certes, mais avec maintenant une bonne compréhension des limites et hypothèses de cette formule. Et ça, j'y tiens!!!

Au passage, on peut remarquer que la pression des fumées baisse plus lentement que celle de l'air extérieur. C'est pas un scoop en soi, certes, mais c'est un peu déconcertant de prime abord.

N'oublions pas que c'est un calcul d'ordre de grandeur. Les fumées ne seront pas statiques. Fort heureusement , sinon on s'étoufferait avec les fumées que l'appareil de combustion bois continue de produire nonobstant.

On va donc boucler nos calculs numériques avec une hypothèse très classique.

(HDS.3) Pour la masse volumique des fumées, on prend la formule de l'air sec (xv=0) à pression Pref.

Notre conduit fait 9m.

Pour notre appareil A avec une température en sortie de buse de 400°C, on aura les résultats suivants :
<T_f> = (400+3)/2 = 201.5°C
<ρ_f> = ρ_ah(P_ref, <T_f>, xv=0) = 101049/8.31/(273.15+201.5)*28.97 = 0.74 kg/m3
dP = (1.27-0.74)*9.81*9 = 47 Pa
Pour notre appareil B avec une température en sortie de buse de 280°C, on aura les résultats suivants :
<T_f> = (280+3)/2 = 141.5°C
<ρ_f> = ρ_ah(P_ref, <T_f>, xv=0) = 101049/8.31/(273.15+141.5)*28.97 = 0.85 kg/m3
dP = (1.27-0.85)*9.81*9 = 37 Pa

(justification HDS.3) La première chose à noter est que prendre la masse volumique à Pref ou Pref-dP, ça ne joue qu'à la marge. S'il n'y a pas de condensation dans le conduit (j'espère bien!), la masse volumique des fumées sera celle d'un gaz aussi parfait que l'air. C'est à dire qu'on peut reprendre la formule de ρ_ah et simplement substituer la masse molaire de l'air humide avec celle des fumées humides Mf. On a calculé Mf=28.54g/mol dans un précédent article. Autrement dit, l'hypothèse a une précision relative de 28.97/28.54 = 2% près. "Finger in the nose"

Les conclusions qui s'imposent déjà

Pour mémoire, le tirage nominal des appareils A et B est de l'ordre de 10Pa. A cette lumière, le résultat des calculs est clair. Passée la phase d’allumage, on risque plus d’avoir des soucis de surtirage que le contraire. On peut d’ores et déjà arrêter les décisions suivantes :

Nul besoin d’élargissement de la section entre buse de sortie de l’appareil et conduit. Donc tubage.
Et même, tubage au diamètre minimal. Pour la suite des calculs, on considérera un tubage diamètre 120.
Nul besoin d’un extracteur de fumées. Par contre, un modérateur de tirage est envisageable.
A priori, pas besoin d’isoler entre tubage et conduit. Mais cela devra être vérifié plus finement :
- Risque de faire travailler la maçonnerie sous les dilatations différentielles ?
  Pour évaluer cela, il faudra déterminer la température moyenne du conduit maçonné
- Risque de bistrage au niveau de la souche ?
  La souche, contrairement au mur, n’est pas isolée ni protégée du vent. Les fumées ont alors de grandes chances de condenser sur les parois.
  Pour éviter cela, le mieux serait d’isoler la partie du tubage dans l’emprise de la souche.
  - Impossible de déverser ou maçonner un isolant pour n’isoler que la souche. Il faudrait une plaque d’appui vers (ou un peu en-dessous) du pied de la souche.
  - Reste la possibilité –hasardeuse- de réaliser un manchon isolé… Qui ne doit ni s’affaisser, ni relarguer des poussières (fibreuses) indésirables via l’ouverture obligatoire de 20cm² en pied du conduit.
    En théorie, le produit atrogaine fait ça très bien. En pratique, c'est pas évident du tout que ça passe en épaisseur...